Mathematics Advising Guide 2024 - 2025
Mathematics encompasses the study of patterns in nature, the development of tools to understand those patterns, and the generalization of those ideas in an abstract setting. A mathematics degree teaches a student to think, to reason, to experiment, and to learn and grow. Mathematics inspires not only science, technology, and their applications, but all aspects of society.
-
Students learn how to ask good questions, make connections, work with others, explain their thoughts, and find evidence to back up their reasoning.
-
Professors provide a solid foundation in the subject, spark interest in mathematical topics, use technology in learning, use innovative pedagogical approaches, and provide students with resources to pursue research experiences.
-
Graduates leave Gustavus thoroughly prepared for graduate study, secondary school teaching, a life of service, or employment in government or industry.
-
To declare a Mathematics Major, use this form
Mathematics Major Requirements
Click here for the 2023 - 2024 Mathematics Advising Guide.
A grade of C- or higher is necessary in all 11 courses used to satisfy the requirements of the major. If you do not already have credit for MCS-121 (Calculus I) then you will need 12 courses to satisfy the major.
- Mathematics Core (4): These should usually be taken during the first and second years.
- MCS-122 Calculus II (has MCS-121 Calculus I as a prerequisite) and
- MCS-150 Discrete Mathematics and
- MCS-221 Linear Algebra and
- MCS-222 Multivariable Calculus
- Breadth (2): These two courses in related fields add breadth to the mathematics major.
- MCS-142 Introduction to Statistics
- MCS-177 Introduction to Computer Science I
- Writing (1): A transitional course that prepares students for upper-level coursework and mathematical proof-writing. Students must take one of the following courses.
- MCS-213 Algebraic Structures
- MCS-220 Intro to Analysis
- Sequence (2): A sequence of two successive 300 level courses:
- MCS-313 and MCS-314 Algebra or
- MCS-331 and MCS-332 Analysis and Topology or
- MCS-353 and MCS-357 Dynamical Systems
-
Electives (2). Two additional mathematics courses at the 200 or 300 level. Students should consult with their advisors to discuss which courses best fit their needs.
Mathematics Minor Requirements
A grade of C- or higher is necessary in all courses used to satisfy the requirements of the minor.
- Mathematics Core (4): These should usually be taken during the first and second years.
- MCS-122 Calculus II (has MCS-121 Calculus I as a prerequisite) and
- MCS-150 Discrete Mathematics and
- MCS-221 Linear Algebra and
- MCS-222 Multivariable Calculus
- Writing (1): A transitional course that prepares students for upper-level coursework and mathematical proof-writing. Students must take one of the following courses.
- MCS-213 Algebraic Structures
- MCS-220 Intro to Analysis
- Elective (1): One additional mathematics course at the 300 level. Students should consult with their advisors to discuss which courses best fit their needs.
Upcoming Math Course Offerings
The 100-level Core courses (MCS-121, 122, and 150) and Breadth courses (MCS-142 and 177) are offered every semester. Other scheduled course offerings in the major for the next few semesters are:
| Spring 25 | Fall 25 | Spring 26 | Fall 26 | |
|---|---|---|---|---|
| MCS-221 Linear Algebra | MCS-221 Linear Algebra | MCS-222 Multivariable Calculus | MCS-221 Linear Algebra | |
| MCS-213 Algebraic Structures | MCS-220 Intro to Analysis | MCS-213 Algebraic Structures | MCS-220 Intro to Analysis | |
| MCS 250 Discrete Math II | MCS-253 Differential Equations | MCS 250 Discrete Math II | MCS-253 Differential Equations | |
| MCS 314 Algebra II | MCS-331 Real Analysis | MCS-332 Topology | MCS-313 Algebra I | |
| MCS-353 Continuous Dynamics | MCS-357 Discrete Dynamics | MCS-303 Geometry | MCS-321 Complex Analysis |
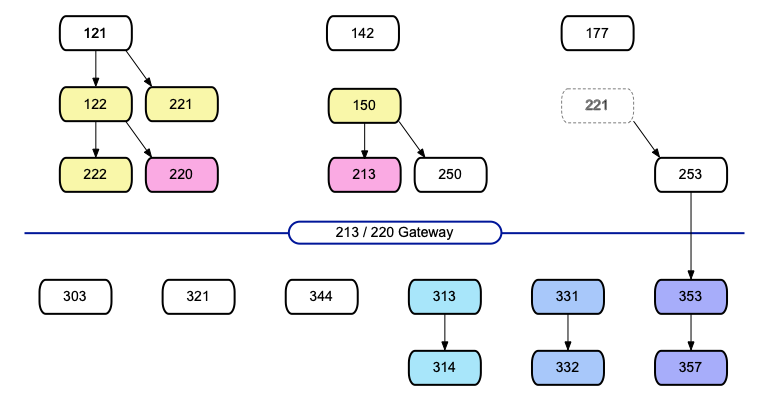
Course Dependencies
Arrows show prerequisites. All courses below the "Gateway" line require completion of a Writing course (213 or 220) as a prerequisite. MCS-221 (Linear Algebra) is a prerequisite for MCS-253.
Honors Program
In order to graduate with Honors in Mathematics, a student must complete an application for admission to the Honors program, available through the department chair, showing that the student satisfies the admission requirements, and then the requirements of the program.
The requirements for admission to the Honors program are as follows:
- Completion of steps 1 - 3 of the Mathematics Major with a grade point average greater than 3.14.
- Approval by the Mathematics Honors committee of an Honors thesis proposal. (Guidelines are available in the Mathematics Advising Guide.)
The requirements of the honors program after admission are as follows:
- Attainment of a GPA greater than 3.14 in courses used to satisfy the requirements of the major. If a student has taken more courses than the major requires, that student may designate for consideration any collection of courses satisfying the requirements of the major.
- Approval by the Mathematics Honors Committee of an Honors thesis. The thesis should conform in general outline to the previously approved proposal (or an approved substitute proposal), should include approximately 160 hours of work, and should result in an approved written document. Students completing this requirement will receive credit for the course MCS-350, whether or not they graduate with Honors. (See the Mathematics Advising Guide for the thesis guidelines.)
- Oral presentation of the thesis in a public forum, such as the departmental seminar. This presentation will not be evaluated as a criterion for thesis approval, but is required.
Honors Thesis Guidelines
Mathematics honors thesis proposals should be written in consultation with the faculty member who will be supervising the work. The proposal and thesis must each be approved by the Mathematics Honors Committee. These guidelines are intended to help students, faculty supervisors, and the committee judge what merits approval.
The thesis should include creative work, and should not reproduce well-known results; however, it need not be entirely novel. It is unreasonable for an undergraduate with limited time and library resources to do a thorough search of the literature, such as would be necessary to ensure complete novelty. Moreover, it would be rare for any topic to be simultaneously novel, easy enough to think of, and easy enough to do.
The thesis should include use of primary-source reference material. As stated above, an exhaustive search of the research literature is impractical. None the less, the resources of inter-library loan, the faculty supervisor's private holdings, etc. must be tapped if the thesis work is to go beyond standard classroom/textbook work.
The written thesis should sufficiently explain the project undertaken and results achieved that someone generally knowledgeable about mathematics, but not about the specific topic, can understand it. The quality of writing and care in citing sources should be adequate for external distribution without embarrassment.
The thesis must contain a substantial mathematical component, though it can include other disciplines as well. If a single thesis simultaneously satisfies the requirements of this program and some other discipline's honors program, it can be used for both (subject to the other program's restrictions). However, course credit will not be awarded for work which is otherwise receiving course credit.
The Mathematics Honors Committee will maintain a file of past proposals and theses, which may be valuable in further clarifying what constitutes a suitable thesis. In order to provide some guidance of the sort before the program gets under way, here are some possible topics that appear on the surface to be suitable:
- A student could study the history surrounding Fermat's last theorem, and discuss and explain past failed attempts and the recent successful attempt to prove this theorem.
- A student could research the topic of knot theory and discuss the implications of this theory to the study of DNA and other biological materials.
- A student could study the use of wavelets in signal analysis, and the general usefulness of orthonormal families of functions in signal analysis.
Math Major FAQ
How much time does the major take?
- You need 11 or 12 classes, depending on your background in Calculus.
- It's feasible to complete the major in six semesters, with no more than two major courses per semester, even if you haven't had calculus before. It's okay if you don't start the major immediately! But you probably do need at least six semesters once you get started.
- Starting early and spreading your major courses over seven or eight semesters means you'll have more flexibility to choose your electives, or to pursue a second major.
What's the overall timeline like (for the major)?
- Aim to complete the Core requirements (MCS-122, 222, 221, and 150) within 3 or 4 semesters.
- Your Writing course (MCS-213 or 220) probably belongs in your 4th or 5th semester. It might come earlier for students with a strong background in mathematics.
- You'll declare your major and get an academic advisor in the MCS department around the time you're taking your Writing course
- Your Sequence and Elective courses come after that, and your advisor will help you choose and schedule them.
- The Breadth courses (MCS-142 and 177) do not have prerequisites and are not required for other courses in the major. It's nice to take care of them early, but they can be fitted into your schedule whenever it's convenient.
Where should I start? What comes next?
- Take care of the Core requirements first. Good starting points are MCS-150 (Discrete Math) and/or a Calculus course (MCS-121, 122, or 222) that you don't already have credit for.
- If you're currently in a math course, ask your instructor about a good course to take next.
- If you don't feel ready to take Calculus I and know you need more pre-calculus review, talk to an instructor in the MCS department. We don't currently offer a pre-calculus course, but we can point you to other resources to help you prepare.
Can I study abroad?
- Students wishing to study abroad should speak with their advisors to discuss courses and study abroad programs.
- Study abroad programs can be found on the Center for International and Cultural Education page.
Additional Questions
Should I take MCS-213 (Algebraic Structures) or MCS-220 (Intro to Analysis)?
- Take only one of these courses, not both.
- Both courses teach proof-writing, problem-solving, and common mathematical foundations that will be useful in all your upper-level math courses.
- The main difference is that 213 includes some topics from modern algebra (groups, rings, and fields), while 220 includes some topics from real analysis (the real number line and the foundations of calculus).
- If you don't have a preference as to the topic. you can just choose whichever one fits your schedule best. 213 runs in the spring, while 220 runs in the fall.
- Either course will prepare you for upper-level coursework, so there's no need to worry about taking the "wrong" one.
What is MCS-150 (Discrete Math)? Should I take it?
- Discrete Math is a QUANT course and is required for Computer Science, Math, and Statistics majors.
- Compared to Calculus, Discrete Math covers a greater variety of simpler topics.
- Compared to Calculus Discrete Math places a greater emphasis on logic, reasoning, conjecture, and proof (and less emphasis on computation).
What is MCS-115 (Nature of Math)? Should I take it?
- Nature of Math is required for the Elementary Education major
- Nature of Math is a good choice if you need a QUANT credit, and you don't need Calculus or Discrete Math for your intended major.