Absorption Spectra of Conjugated Dyes

AbsorptionSpectraofConjugatedDyes

�� In this investigation you will measure the absorption spectra of a series of cyanine dyes.� Your experimental observations will be examined in the framework of a simple quantum mechanical model, the particle in a box model.� Prior to the laboratory you should familiarize yourself with the structures of the molecules to be studied.�

Experimental Method:

The dyes you will be using in this experiment are toxic.� You should be careful in working with them, and avoid getting the solutions on your skin.� In addition, these dyes will slowly degrade in the presence of light, so you should keep the solutions in the dark when they are not in use.� The manufacturers claim 97% purity for the three dyes listed below.� You should obtain spectra of the three cyanine dyes indicated in Table 1.

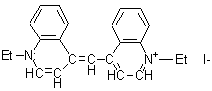1,1 '-diethyl-4,4'-cyanine iodide

Table 1.

Dye	M.W. (g mol^-1)	e(10⁵M^-l cm^-l)^a	P
1,1 '-diethyl-2,2'-cyanine iodide	454.4	0.75	3
1,1'-diethyl-2,2'-carbocyanine iodide	480.4	1.95	5
1,1 '-diethyl-2,2'-dicarbocyanine iodide	506.4	2.13	7

^aMolar absorption coefficient in methanol at the absorption maximum (from reference 2).

P = # of carbon atoms in chain of conjugation.

N = P + 3 = # of conjugated � electrons in cyanine chain

�� We will use methanol as the solvent.� The molar absorptivities (extinction coefficients) of these dyes are quite high, so plan your dilutions to minimize the use of the solutes and solvent.� Choose final concentrations such that A~0.5-1.0 for a standard, 1-cm pathlength cuvette. (Remember Beer's Law: A = ecl.).� Record spectra against a solvent reference, scanning from 400-800 nm.� Note the colors of the stock solutions and any changes in color that occur when the solutions are diluted.� You will be using the Ocean Optics UV-Visible spectrometer to record the spectrum of each dye.

�� Draw these molecules in HyperChem and using a semiempirical CI calculation calculate the electronic spectrum.� Place this spectrum in your notebook.� What does the structure look like?�� Explore the molecular orbitals of this series of compounds.

�� Determine how the particle in a box formulation can explain the absorption spectra of these dyes in the free electron model.� Develop a formula on this basis.

Analysis:

�� Your computer notebook should include a concise summary of the data, i.e., a table comparing your measurements of l_max with the l_max determined from the free electron model.� In comparing experiment and theory, the wavelength of maximum absorption first should be calculated with a = 0, i.e., no adjustment for end effects.� You then should fit the data to the best possible a, using a non-linear least squares fit within SigmaPlot (Regression Wizard- Equation Category � User-Defined).� Record data on the quality of the fit as indicated by Sigma Plot.� You also should analyze the l_max for the members of the 1,1'-diethyl-4,4'-cyanine iodide series listed in Table 2. (data obtained from Fisher and Hamer).

Table 2.

Dye	l_max	P
1,1'-diethyl-4,4'-cyanine iodide	593	7
1,1 '-diethyl-4,4'-carbocyanine iodide	704	9
1,1'-diethyl-4,4'-dicarbocyanine iodide	810	11
1,1 '-diethyl-4,4'-tricarbocyanine iodide	932	13

P # of carbon atoms in chain of conjugation

N = P + 3 = # of conjugated ir electrons in cyanine chain

�� As with the 2,2' series, use the free electron model to calculate the l_max�s with a = 0 and with the best a determined by a non-linear least squares fit. (Do not despair if your a's lie somewhat outside the 0 <a< 1 range.)

�� As part of a brief discussion, compare the a's for the two series and try to explain any differences based on differences in the molecular structures.� You also should comment on the appropriateness of the free electron/particle-in-a-box model for describing the spectra of the cyanine dyes.� Your answer to this question should go beyond simply stating whether the model is "good" or "bad."

References:

1.�� N.I. Fisher and F.M. Hamer, Proc. Roy. Soc., Series A 154, 703 (1936).

2.�� S.E. Sheppard, and A.L. Geddes, J. Am. Chem. Soc. 66, 2003 (1944).

3.�� H. Kuhn, J. Chem. Phys. 17, 1198 (1949).

4.�� J.R. Platt, J. Chem. Phys. 22, 1448 (1954).

5.�� W. West, and S. Pearce, J. Phys. Chem. 69, 1894 (1965).