MCS-388 Homework 6 (Spring 2005)
Due: May 6, 2005
Do one, and only one, of the following problems; you may choose either:
-
For the theorist:
-
Prove that no node that is latest is
up-safe, using the definitions of those terms given in the
handout on partial redundancy elimination. You will presumably
want to first show that no node that is earliest is
up-safe, then use that to show that no node that is delay is
up-safe (see below), and then finally use that to (trivially)
show that no node that is latest is up-safe. Note: in
showing that no delay node is up-safe, you may assume that
all nodes are reachable from the start node.
- For the practitioner:
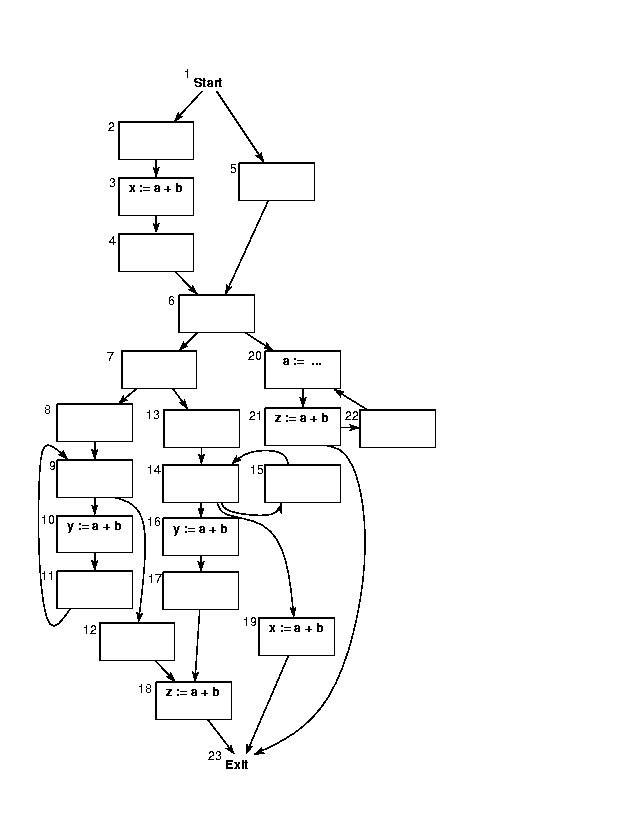
- Subject the flow graph shown below
to the dataflow analyses described in the handout on
partial redundancy elimination, using
a+b as the expression in question.
Which nodes are down-safe? Up-safe? Earliest? Delay? Latest? Which
nodes should a+b be computed at the beginning of?
Course web site: http://www.gac.edu/~max/courses/S2005/MCS-388/
Instructor: Max Hailperin <max@gustavus.edu>

