Raman Spectroscopy
When light passes through a medium a portion of this light is scattered.
Most of the scattered light is elastically scattered and thus without change in
wavelength (no change in energy of a photon). This type of scattering is
called Rayleigh scattering. If the light is monochromatic and of high
intensity as is available in a laser beam then a portion of the light will be
scattered inelestically with a shift in wavelength. In 1928, physicist C.
V. Raman and his associate Krishnan discovered this effect and latter received
the 1930 Nobel prize in
physics for this work. The inelastic scattering and the resulting
shift in wavelength of the scattered photon is known as the Raman effect.
With the availability of lasers, Raman spectroscopy has become a more sensitive
and useful form of spectroscopy. Raman spectroscopy can provide
information that is complementary to infrared spectroscopy but as well has many
variants, including resonance Raman spectroscopy, that provide further insights
into molecular geometry and electronic structure. Raman spectra are
recorded by monitoring the intensity of Raman scattering as a function of
wavelength. The frequency of the molecular state corresponding to the
spectral feature is given by Dn.
In
order for a vibrational mode of a molecule to be active in the Raman spectrum
it must induce an oscillating polarizability, a.
This differs from infrared active vibrational modes that must produce an
oscillating dipole moment. Since light scattering depends strongly on
polarization, it is important to consider the polarization of the incident
light beam and the polarization of the scattered light beam. Some scattered
radiation will have the same polarization as the incident beam and is thus
considered to have parallel polarization. This can be monitored
experimentally by using a polarizer to measure the intensity of scattered light
with the same polarization at right angles to the incident beam. The
depolarization of the incident beam resulting from scattering can be determined
by detecting scattered light (again at right angles) through a polarizer at 90°
to the incident polarization vector, 
. The depolarization
ratio is the ratio of the intensity of scattered radiation from a particular
spectral feature with measured perpendicular divided by that with parallel
polarization.
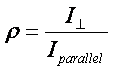
The depolarization ratio depends on the symmetry of the vibrational mode which corresponds to the band under investigation. For any nontotally symmetric vibration r=3/4 and for totally symmetric modes r<3/4. In CCl4 (Td point group), for example, the totally symmetric C-Cl stretch at 459 cm-1 has a r near zero.
The rotational selection rule for Raman is DJ = 0, ±2 (compared to DJ = 0, ±1 for infrared) because Raman scattering is a two-photon process resulting in the angular momentum changing by zero or two units. For many spectra the primary interest is in examining the vibrational details. In Raman spectroscopy the vibrational selection rule is Dv = ±1, ±2, …
The intensity of scattering depends on the differential cross-section (signal is only collected through a small solid angle).
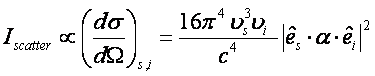
Where ns is the frequency (in Hz) of the incident radiation,
ni is the frequency of the
scattered radiation, a is the
polarizability tensor, and is the polarization
vector of the incident radiation. It is worth noting that Raman scattering
will be substantially more intense as the wavelength of the incident radiation
becomes shorter (thus the frequency becomes higher).
The polarizability is a tensor constructed from the components aZZ, aXZ, etc..
Where the z-axis is the lab-frame incident radiation polarization.